TEKS Standards and Student Expectations

A(10) Number and algebraic methods. The student applies the mathematical process standards and algebraic methods to rewrite in equivalent forms and perform operations on polynomial expressions. The student is expected to:

A(10)(E) factor, if possible, trinomials with real factors in the form ax² + bx + c including perfect square trinomials of degree two

A(10)(F) decide if a binomial can be written as the difference of two squares and if possible, use the structure of a difference of two squares to rewrite the binomial

A(10)(D) rewrite polynomial expressions of degree one and degree two in equivalent forms using the distributive property

A(8) Quadratic functions and equations. The student applies the mathematical process standards to solve, with and without technology, quadratic equations and evaluate the reasonableness of their solutions. The student formulates statistical relationships and evaluates their reasonableness based on real-world data. The student is expected to:

A(8)(A) solve quadratic equations having real solutions by factoring, taking square roots, completing the square, and applying the quadratic formula

Resource Objective(s)

The student will use a variety of methods to solve problems by factoring, including models, guess and check, grouping, and special cases.

Essential Questions

What is the process for factoring a trinomial with a leading coefficient of 1?

What is the process for factoring a trinomial when the leading coefficient is not 1?

How can you determine if the rules for difference of two squares, difference of two cubes, or perfect squares can be used to factor?

When does the grouping method for factoring apply?

Vocabulary

• Binomial
• Factor
• GCF (Greatest Common Factor)
• Leading Coefficient
• Trinomial
• Polynomial
• Quadratic Equation

One way to find the factors of a value is to use models to create a rectangle. The length and width represent the factors.

Example 1: Factors of 12 can be shown three different ways. 

12 has a total of 6 different factors: 1, 2, 3, 4, 6, and 12.

Example 2: Algebraic expressions can also be factored using algebra tiles to create rectangles. In the example below, 2x + 4 is used to create a rectangle. 

As you can see, the length and width of the rectangle represent the factors of 2x + 4. The length is (x + 2) and the width is 2. 

The factors of 2x + 4 are 2 and (x + 2).

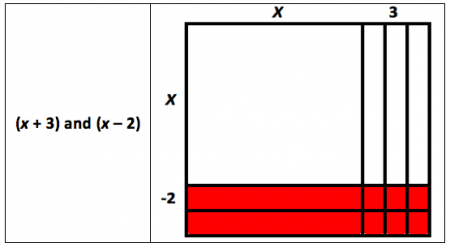
Example 3: Trinomials can also be factored using algebra tiles. The trinomial x² + x - 6 can be modeled by the following rectangle.

The side lengths of the rectangle show the factors of x² + x - 6 are (x + 3) and (x - 2).

When you are ready, complete the two practice examples below to check your understanding.

Always check to see if you can factor something out!

The first rule to factoring is to find the greatest common factor (GCF) of each term in the polynomial.

• If there is any factor in common in the polynomial, divide each term by that factor.
• Then, rewrite the polynomial using the distributive property with the common factor on the outside of the parenthesis.

Example:

$2x^3- 2x^2-12x$

All terms in the example have a coefficient that is divisible by 2. Each term also has an x. Therefore, the GCF is 2x.

When 2x is factored out and the distributive property is applied the result is 

$2x(x^2- x - 6)$.

Check your understanding with the two practice examples below.

Binomials

If you are given a binomial to factor, the first special product to check for is the difference of two squares.

Difference of Two Squares:

 $a^2-b^2= (a - b)(a + b)$.

If both terms are separated by a subtraction symbol and they are both perfect squares, the square roots can be used to write the factors.

Example 1: Factor $4x^2-9y^2$:

• The terms are separated by a subtraction symbol.
• Both terms are perfect squares.

   $(2x{)}^2 and (3y{)}^2$

According to the rule for the difference of two squares, the factors will be $(2x-3y)(2x+3y)$.

Trinomials

If you are given a trinomial to factor, the first special product to check for is a perfect square trinomial.

Perfect Square Trinomials:

$a^2+2ab+b^2 = (a+b{)}^2 or a^2-2ab+b^2 = (a-b{)}^2$

If the first term is a square, the last term is a square, and the middle term is two times the square root of the first and the last term, then it is a perfect square. There are two forms: one with a positive middle term and one with a negative middle term.

Example 2: Factor $x^2+6x+9$

Notice the first and last terms are both perfect squares. When you multiply the square roots of x and 3 times 2, you get 6x which is the middle term. According to the rule, the factors are 

$(x+3)(x+3) or (x+3{)}^2$

Example 3: Factor $4x^2-20x+25$

Notice the first and last terms are both perfect squares. When you multiply the square roots of 2x and 5 times -2, you get -20x which is the middle term. According to the rule, the factors are 

$(2x-5)(2x-5) or (2x-5{)}^2$

Check your understanding by completing the practice example below. Determine which polynomials can be factored with a special product rule. Match each polynomial with the type of special product (first blank) and its factors (second blank).

After checking for a GCF and Special Products, look for polynomials with three terms that have a leading coefficient of 1. If the leading coefficient is 1, put x's as the first term in each set of parentheses. Then you factor the last term and find the two factors that add or subtract to make the middle term.

Use the practice example to complete the activity below.

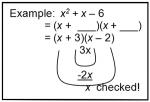
If the leading coefficient is not 1, you factor both the first and last terms and find the two products that add or subtract to make the middle term. Check your answer by using the smiley face check.

Use the practice example to complete the activity below.

If there are four or more terms, you need to group them together, and then factor each part.

You can do this two ways—either by using the box method or parentheses.

Box Method: 

1. Put all four terms in a two by two box.
2. Look for the GCF in each column and row.
3. Include signs for each of the factors.
4. The result will be two factors: one on the length and the other on the width.

Parentheses Method: 

1. Put parentheses around the first two terms and another set around the last two terms.
2. Find the GCF of each set of parentheses. 
3. Once the GCF is factored out, the terms inside each set of parentheses should match. 
4. The factors will be the terms inside the parentheses (from step 3) and the GCF outside each set of parentheses (in step 2). 

Check your understanding by factoring the following polynomial (using either method) and answer the questions below. 

Some problems may ask for the solution of a quadratic equation. To solve these problems, set the factors equal to 0 and solve for x. 

Example: 

  $$\begin{gathered} 2x^3 - 2x^2 -12x \\ = 2x (x^2 - x - 6) \\ = 2x (x - 3)(x + 2) \end{gathered}$$

To solve this problem, you would need to set all factors to 0 and solve for x. There will be three solutions.

Fill in the blanks below to find the three solutions to the polynomial. 

Check polynomials in your graphing calculator:

Your solutions will be the x-intercepts on the graph.

• Input your equation using the equation editor [Y =] key on the graphing calculator.
• Press [GRAPH].
• Press [2nd] [TRACE] to access the CALC menu.
• Press [2] to select the zero command.
• Use the arrow keys to select a left bound and a right bound.