Components of Vectors

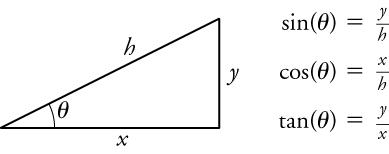
For the analytical method of vector addition and subtraction, we use some simple geometry and trigonometry, instead of using a ruler and protractor as we did for graphical methods. However, the graphical method will still come in handy to visualize the problem by drawing vectors using the head-to-tail method. The analytical method is more accurate than the graphical method, which is limited by the precision of the drawing. For a refresher on the definitions of the sine, cosine, and tangent of an angle, see Figure 5.18.

Figure 5.18 For a right triangle, the sine, cosine, and tangent of θ are defined in terms of the adjacent side, the opposite side, or the hypotenuse. In this figure, x is the adjacent side, y is the opposite side, and h is the hypotenuse.

Since, by definition, $\text{cos}\theta =x/h$, we can find the length x if we know h and $\theta$ by using $x=h\text{cos}\theta$. Similarly, we can find the length of y by using $y=h\text{sin}\theta$. These trigonometric relationships are useful for adding vectors.

When a vector acts in more than one dimension, it is useful to break it down into its x and y components. For a two-dimensional vector, a component is a piece of a vector that points in either the x- or y-direction. Every 2-d vector can be expressed as a sum of its x and y components.

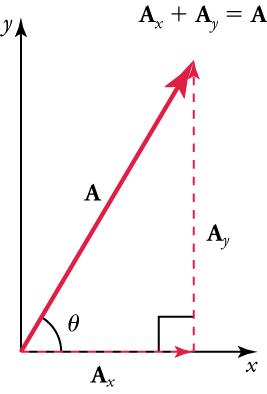
For example, given a vector like$A$in Figure 5.19, we may want to find what two perpendicular vectors,$A_x$and$A_y$, add to produce it. In this example,$A_x$and$A_y$form a right triangle, meaning that the angle between them is 90 degrees. This is a common situation in physics and happens to be the least complicated situation trigonometrically.

Figure 5.19 The vector$A$, with its tail at the origin of an x- y-coordinate system, is shown together with its x- and y-components,$A_x$and$A_y.$These vectors form a right triangle.

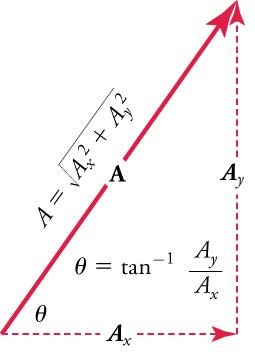
$A_x$and$A_y$are defined to be the components of$A$along the x- and y-axes. The three vectors,$A$,$A_x$, and$A_y$, form a right triangle.

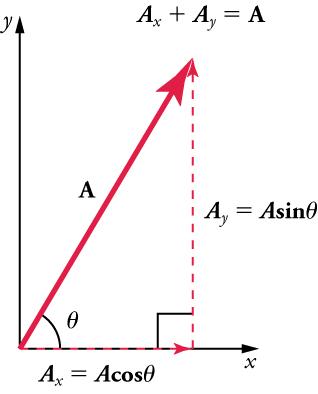
If the vector$A$is known, then its magnitude$A$(its length) and its angle$\theta$(its direction) are known. To find$A_x$and$A_y$, its x- and y-components, we use the following relationships for a right triangle:

and

where$A_x$is the magnitude of A in the x-direction,$A_y$is the magnitude of A in the y-direction, and$\theta$is the angle of the resultant with respect to the x-axis, as shown in Figure 5.20.

Figure 5.20 The magnitudes of the vector components$A_x$and$A_y$can be related to the resultant vector$A$and the angle$\theta$with trigonometric identities. Here we see that$A_x=A\text{cos}\theta$and$A_y=A\text{sin}\theta .$

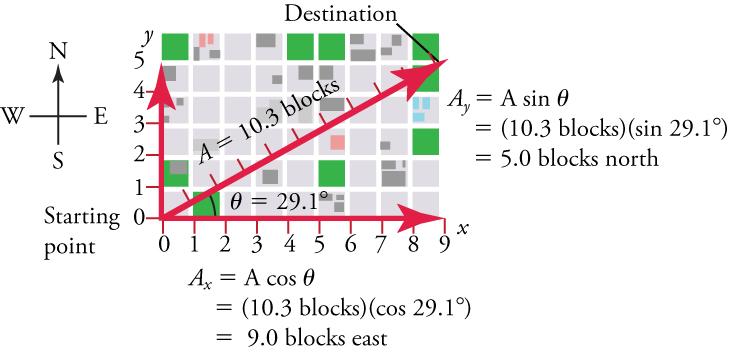
Suppose, for example, that$A$is the vector representing the total displacement of the person walking in a city, as illustrated in Figure 5.21.

Figure 5.21 We can use the relationships $A_x=A\text{cos}\theta$ and $A_y=A\text{sin}\theta$ to determine the magnitude of the horizontal and vertical component vectors in this example.

Then A = 10.3 blocks and $\theta ={29.1}^{\circ }$, so that

This magnitude indicates that the walker has traveled 9 blocks to the east—in other words, a 9-block eastward displacement. Similarly,

indicating that the walker has traveled 5 blocks to the north—a 5-block northward displacement.

Analytical Method of Vector Addition and Subtraction

Calculating a resultant vector (or vector addition) is the reverse of breaking the resultant down into its components. If the perpendicular components $A_x$ and $A_y$ of a vector $A$ are known, then we can find $A$ analytically. How do we do this? Since, by definition,

we solve for $\theta$ to find the direction of the resultant.

Since this is a right triangle, the Pythagorean theorem (x² + y² = h²) for finding the hypotenuse applies. In this case, it becomes

Solving for A gives

In summary, to find the magnitude $A$ and direction $\theta$ of a vector from its perpendicular components $A_x$ and $A_y$, as illustrated in Figure 5.22, we use the following relationships:

Figure 5.22 The magnitude and direction of the resultant vector$A$can be determined once the horizontal components$A_x$and$A_y$have been determined.

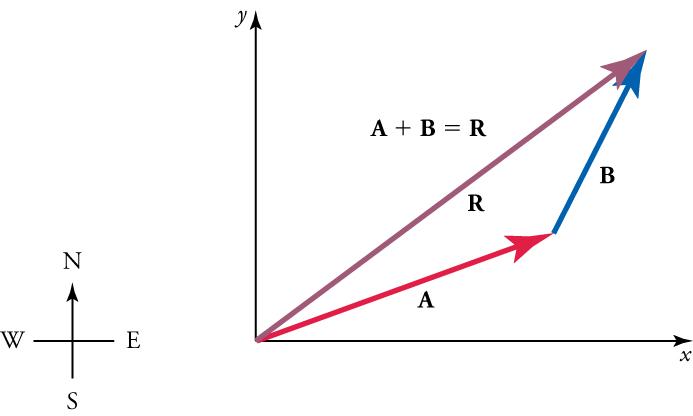
Sometimes, the vectors added are not perfectly perpendicular to one another. An example of this is the case below, where the vectors $A$ and $B$ are added to produce the resultant $R\text{,}$ as illustrated in Figure 5.23.

Figure 5.23 Vectors$A$and$B$are two legs of a walk, and$R$is the resultant or total displacement. You can use analytical methods to determine the magnitude and direction of$R$.

If$A$and$B$represent two legs of a walk (two displacements), then$R$is the total displacement. The person taking the walk ends up at the tip of$R$. There are many ways to arrive at the same point. The person could have walked straight ahead first in the x-direction and then in the y-direction. Those paths are the x- and y-components of the resultant,$R_x$and$R_y.$If we know$R_x$and$R_y$, we can find$R$and$\theta$using the equations$R=\sqrt{R_{\text{x}}{}^2+R_{\text{y}}{}^2}$and$\theta =ta{n}^{–1}(R_y/R_x)$.

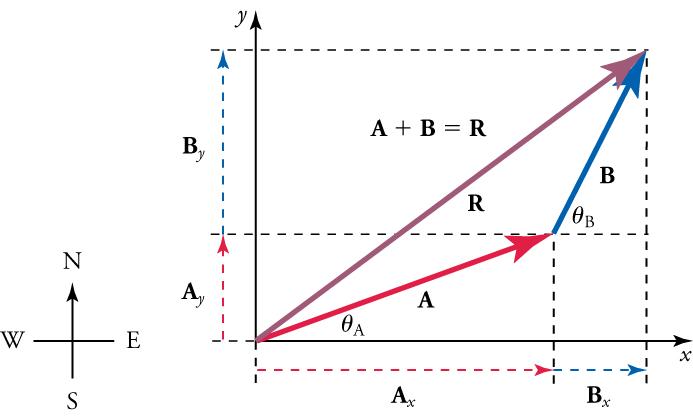
1. Draw in the x and y components of each vector (including the resultant) with a dashed line. Use the equations$A_x=A\text{cos}\theta$and$A_y=A\text{sin}\theta$to find the components. In Figure 5.24, these components are$A_x$,$A_y$,$B_x$, and$B_y.$Vector$A$makes an angle of${\theta }_A$with the x-axis, and vector$B$makes and angle of${\theta }_B$with its own x-axis (which is slightly above the x-axis used by vector A).

   

   Figure 5.24 To add vectors$A$and$B,$first determine the horizontal and vertical components of each vector. These are the dotted vectors$A_x,$$A_y$$B_y$shown in the image.
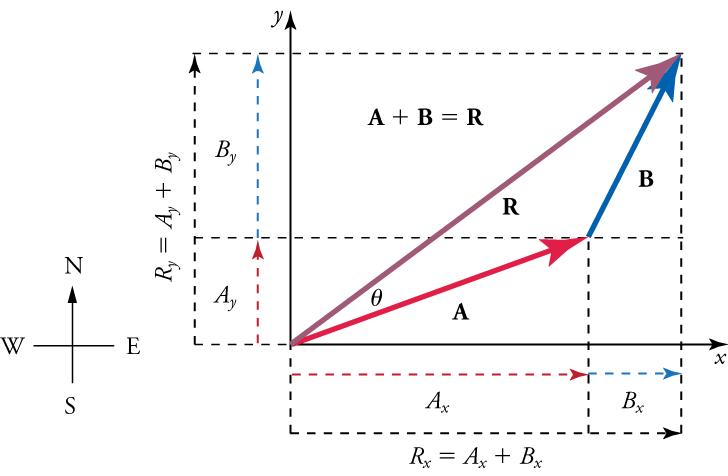
2. Find the x component of the resultant by adding the x component of the vectors
   $$R_x=A_x+B_x$$

   and find the y component of the resultant (as illustrated in Figure 5.25) by adding the y component of the vectors.

   $$R_y=A_y+B_y\text{.}$$

   

   Figure 5.25 The vectors$A_x$and$B_x$add to give the magnitude of the resultant vector in the horizontal direction,$R_{\text{x}}.$Similarly, the vectors$A_y$and$B_y$add to give the magnitude of the resultant vector in the vertical direction,$R_{\text{y}}.$

   Now that we know the components of $R,$ we can find its magnitude and direction.

3. To get the magnitude of the resultant R, use the Pythagorean theorem.
   $$R=\sqrt{R_x^2+R_y^2}$$
4. To get the direction of the resultant
   $$\theta ={\tan }^{-1}(R_y/R_x)\text{.}$$

Using the Analytical Method of Vector Addition and Subtraction to Solve Problems

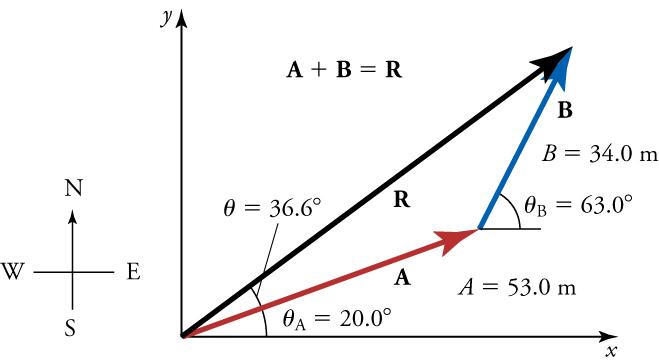
Figure 5.26 uses the analytical method to add vectors.

Worked Example

An Accelerating Subway Train

Add the vector$A$to the vector$B$shown in Figure 5.26, using the steps above. The x-axis is along the east–west direction, and the y-axis is along the north–south directions. A person first walks$\text{53}\text{.0 m}$in a direction$\text{20}\text{.0°}$north of east, represented by vector$A.$The person then walks$\text{34}\text{.0 m}$in a direction$\text{63}\text{.0}°$north of east, represented by vector$B.$

Figure 5.26 You can use analytical models to add vectors.

Strategy

The components of$A$and$B$along the x- and y-axes represent walking due east and due north to get to the same ending point. We will solve for these components and then add them in the x-direction and y-direction to find the resultant.

Solution

First, we find the components of$A$and$B$along the x- and y-axes. From the problem, we know that$A=53.0\text{ m}$,${\theta }_{\text{A}}={20.0}^{\circ }$,$B$=$\text{34}\text{.0 m}$, and${\theta }_{\text{B}}={63.0}^{\circ }$. We find the x-components by using$A_x=A\cos \theta$, which gives

$$\begin{array}{ccc}\hfill A_x& =& A\cos {\theta }_A=(53.0\text{ m})(\cos {20.0}^{\circ })\hfill \\ & =& (53.0\text{ m})(0.940)=49.8\text{ m}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill B_x& =& B\cos {\theta }_B=(34.0\text{ m})(\cos {63.0}^{\circ })\hfill \\ & =& (34.0\text{ m})(0.454)=15.4\text{ m.}\hfill \end{array}$$

Similarly, the y-components are found using$A_y=A\sin {\theta }_A$

$$\begin{array}{ccc}\hfill A_y& =& A\sin {\theta }_A=(53.0\text{ m})(\sin {20.0}^{\circ })\hfill \\ & =& (53.0\text{ m})(0.342)=18.1\text{ m}\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill B_y& =& B\sin {\theta }_B=(34.0\text{ m})(\sin {63.0}^{\circ })\hfill \\ & =& (34.0\text{ m})(0.891)=30.3\text{ m}\text{.}\hfill \end{array}$$

The x- and y-components of the resultant are

$$R_x=A_x+B_x=49.8\text{ m}+15.4\text{ m}=65.2\text{ m}$$

and

$$R_y=A_y+B_y=18.1\text{ m}+30.3\text{ m}=48.4\text{ m}.$$

Now we can find the magnitude of the resultant by using the Pythagorean theorem

5.8$$R=\sqrt{R_x^2+R_y^2}=\sqrt{{(65.2)}^2+{(48.4)}^2}\text{ m}$$

so that

$$R=\sqrt{6601\text{ m}}=81.2\text{ m }\text{.}$$

Finally, we find the direction of the resultant

$$\theta ={\tan }^{-1}(R_y/R_x)=+{\tan }^{-1}(48.4/65.2).$$

This is

$$\theta ={\tan }^{-1}(0.742)={36.6}^{\circ }.$$

Discussion

This example shows vector addition using the analytical method. Vector subtraction using the analytical method is very similar. It is just the addition of a negative vector. That is,$\text{A}-\text{B}\equiv \text{A}+(-\text{B})$. The components of –$\text{B}$are the negatives of the components of$\text{B}$. Therefore, the x- and y-components of the resultant$\text{A}-\text{B}=\text{R}$ are

$$R_x=A_x+-B_x$$

and

$$R_y=A_y+-B_y$$

and the rest of the method outlined above is identical to that for addition.

Links To Physics

Atmospheric Science

Figure 5.27 This picture shows Bert Foord during a television Weather Forecast from the Meteorological Office in 1963. (BBC TV)

Atmospheric science is a physical science, meaning that it is a science based heavily on physics. Atmospheric science includes meteorology (the study of weather) and climatology (the study of climate). Climate is basically the average weather over a longer time scale. Weather changes quickly over time, whereas the climate changes more gradually.

The movement of air, water and heat is vitally important to climatology and meteorology. Since motion is such a major factor in weather and climate, this field uses vectors for much of its math.

Vectors are used to represent currents in the ocean, wind velocity and forces acting on a parcel of air. You have probably seen a weather map using vectors to show the strength (magnitude) and direction of the wind.

Vectors used in atmospheric science are often three-dimensional. We won’t cover three-dimensional motion in this text, but to go from two-dimensions to three-dimensions, you simply add a third vector component. Three-dimensional motion is represented as a combination of x-, y- and z components, where z is the altitude.

Vector calculus combines vector math with calculus, and is often used to find the rates of change in temperature, pressure or wind speed over time or distance. This is useful information, since atmospheric motion is driven by changes in pressure or temperature. The greater the variation in pressure over a given distance, the stronger the wind to try to correct that imbalance. Cold air tends to be more dense and therefore has higher pressure than warm air. Higher pressure air rushes into a region of lower pressure and gets deflected by the spinning of the Earth, and friction slows the wind at Earth’s surface.

Finding how wind changes over distance and multiplying vectors lets meteorologists, like the one shown in Figure 5.27, figure out how much rotation (spin) there is in the atmosphere at any given time and location. This is an important tool for tornado prediction. Conditions with greater rotation are more likely to produce tornadoes.

Grasp Check

Why are vectors used so frequently in atmospheric science?

1. Vectors have magnitude as well as direction and can be quickly solved through scalar algebraic operations.
2. Vectors have magnitude but no direction, so it becomes easy to express physical quantities involved in the atmospheric science.
3. Vectors can be solved very accurately through geometry, which helps to make better predictions in atmospheric science.
4. Vectors have magnitude as well as direction and are used in equations that describe the three dimensional motion of the atmosphere.