Print Resource

Diffraction and Interference

We know that visible light is the type of electromagnetic wave to which our eyes responds. As we have seen previously, light obeys the equation

where $c=3.00\times {10}^8$ m/s is the speed of light in vacuum, f is the frequency of the electromagnetic wave in Hz (or s^–1), and $\lambda$ is its wavelength in m. The range of visible wavelengths is approximately 380 to 750 nm. As is true for all waves, light travels in straight lines and acts like a ray when it interacts with objects several times as large as its wavelength. However, when it interacts with smaller objects, it displays its wave characteristics prominently. Interference is the identifying behavior of a wave.

In Figure 17.2, both the ray and wave characteristics of light can be seen. The laser beam emitted by the observatory represents ray behavior, as it travels in a straight line. Passing a pure, one-wavelength beam through vertical slits with a width close to the wavelength of the beam reveals the wave character of light. Here we see the beam spreading out horizontally into a pattern of bright and dark regions that are caused by systematic constructive and destructive interference. As it is characteristic of wave behavior, interference is observed for water waves, sound waves, and light waves.

Figure 17.2 (a) The light beam emitted by a laser at the Paranal Observatory (part of the European Southern Observatory in Chile) acts like a ray, traveling in a straight line. (credit: Yuri Beletsky, European Southern Observatory) (b) A laser beam passing through a grid of vertical slits produces an interference pattern—characteristic of a wave. (credit: Shim’on and Slava Rybka, Wikimedia Commons)

That interference is a characteristic of energy propagation by waves is demonstrated more convincingly by water waves. Figure 17.3 shows water waves passing through gaps between some rocks. You can easily see that the gaps are similar in width to the wavelength of the waves and that this causes an interference pattern as the waves pass beyond the gaps. A cross-section across the waves in the foreground would show the crests and troughs characteristic of an interference pattern.

Figure 17.3 Incoming waves (at the top of the picture) pass through the gaps in the rocks and create an interference pattern (in the foreground).

Light has wave characteristics in various media as well as in a vacuum. When light goes from a vacuum to some medium, such as water, its speed and wavelength change, but its frequency, f, remains the same. The speed of light in a medium is $v=c/n$, where n is its index of refraction. If you divide both sides of the equation $c=f\lambda$ by n, you get $c/n=v=f\lambda /n$. Therefore, $v=f{\lambda }_n$, where ${\lambda }_n$ is the wavelength in a medium, and

where $\lambda$ is the wavelength in vacuum and n is the medium’s index of refraction. It follows that the wavelength of light is smaller in any medium than it is in vacuum. In water, for example, which has n = 1.333, the range of visible wavelengths is (380 nm)/1.333 to (760 nm)/1.333, or ${\lambda }_n=$285–570 nm. Although wavelengths change while traveling from one medium to another, colors do not, since colors are associated with frequency.

The Dutch scientist Christiaan Huygens (1629–1695) developed a useful technique for determining in detail how and where waves propagate. He used wavefronts, which are the points on a wave’s surface that share the same, constant phase (such as all the points that make up the crest of a water wave). Huygens’s principle states, “Every point on a wavefront is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wavefront is a line tangent to all of the wavelets.”

Figure 17.4 shows how Huygens’s principle is applied. A wavefront is the long edge that moves; for example, the crest or the trough. Each point on the wavefront emits a semicircular wave that moves at the propagation speed v. These are drawn later at a time, t, so that they have moved a distance $s=vt$. The new wavefront is a line tangent to the wavelets and is where the wave is located at time t. Huygens’s principle works for all types of waves, including water waves, sound waves, and light waves. It will be useful not only in describing how light waves propagate, but also in how they interfere.

Figure 17.4 Huygens’s principle applied to a straight wavefront. Each point on the wavefront emits a semicircular wavelet that moves a distance $s=vt$. The new wavefront is a line tangent to the wavelets.

What happens when a wave passes through an opening, such as light shining through an open door into a dark room? For light, you expect to see a sharp shadow of the doorway on the floor of the room, and you expect no light to bend around corners into other parts of the room. When sound passes through a door, you hear it everywhere in the room and, thus, you understand that sound spreads out when passing through such an opening. What is the difference between the behavior of sound waves and light waves in this case? The answer is that the wavelengths that make up the light are very short, so that the light acts like a ray. Sound has wavelengths on the order of the size of the door, and so it bends around corners.

If light passes through smaller openings, often called slits, you can use Huygens’s principle to show that light bends as sound does (see Figure 17.5). The bending of a wave around the edges of an opening or an obstacle is called diffraction. Diffraction is a wave characteristic that occurs for all types of waves. If diffraction is observed for a phenomenon, it is evidence that the phenomenon is produced by waves. Thus, the horizontal diffraction of the laser beam after it passes through slits in Figure 17.2 is evidence that light has the properties of a wave.

Figure 17.5 Huygens’s principle applied to a straight wavefront striking an opening. The edges of the wavefront bend after passing through the opening, a process called diffraction. The amount of bending is more extreme for a small opening, consistent with the fact that wave characteristics are most noticeable for interactions with objects about the same size as the wavelength.

Once again, water waves present a familiar example of a wave phenomenon that is easy to observe and understand, as shown in Figure 17.6.

Figure 17.6 Ocean waves pass through an opening in a reef, resulting in a diffraction pattern. Diffraction occurs because the opening is similar in width to the wavelength of the waves.

The fact that Huygens’s principle worked was not considered enough evidence to prove that light is a wave. People were also reluctant to accept light’s wave nature because it contradicted the ideas of Isaac Newton, who was still held in high esteem. The acceptance of the wave character of light came after 1801, when the English physicist and physician Thomas Young (1773–1829) did his now-classic double-slit experiment (see Figure 17.7).

Figure 17.7 Young’s double-slit experiment. Here, light of a single wavelength passes through a pair of vertical slits and produces a diffraction pattern on the screen—numerous vertical light and dark lines that are spread out horizontally. Without diffraction and interference, the light would simply make two lines on the screen.

When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 17.8 (a). Pure constructive interference occurs where the waves line up crest to crest or trough to trough. Pure destructive interference occurs where they line up crest to trough. The light must fall on a screen and be scattered into our eyes for the pattern to be visible. An analogous pattern for water waves is shown in Figure 17.8 (b). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. Those angles depend on wavelength and the distance between the slits, as you will see below.

Figure 17.8 Double slits produce two sources of waves that interfere. (a) Light spreads out (diffracts) from each slit, because the slits are narrow. The waves overlap and interfere constructively (bright lines) and destructively (dark regions). You can only see the effect if the light falls onto a screen and is scattered into your eyes. (b) The double-slit interference pattern for water waves is nearly identical to that for light. Wave action is greatest in regions of constructive interference and least in regions of destructive interference. (c) When light that has passed through double slits falls on a screen, we see a pattern such as this.

Virtual Physics

Wave Interference

Figure 17.9 Click here for the Wave Interference simulation.

This simulation demonstrates most of the wave phenomena discussed in this section. First, observe interference between two sources of electromagnetic radiation without adding slits. See how water waves, sound, and light all show interference patterns. Stay with light waves and use only one source. Create diffraction patterns with one slit and then with two. You may have to adjust slit width to see the pattern.

Visually compare the slit width to the wavelength. When do you get the best-defined diffraction pattern?

1. when the slit width is larger than the wavelength
2. when the slit width is smaller than the wavelength
3. when the slit width is comparable to the wavelength
4. when the slit width is infinite

Calculations Involving Diffraction and Interference

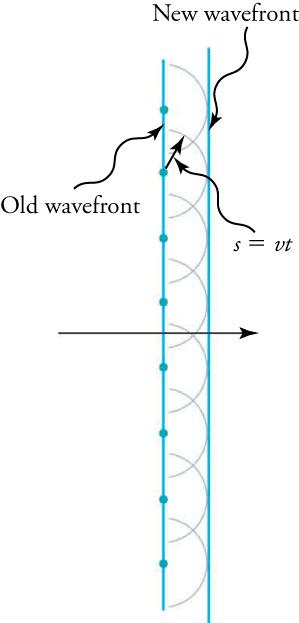
The fact that the wavelength of light of one color, or monochromatic light, can be calculated from its two-slit diffraction pattern in Young’s experiments supports the conclusion that light has wave properties. To understand the basis of such calculations, consider how two waves travel from the slits to the screen. Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they will end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively. If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively. More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths $(\frac{1}{2}\lambda ,\frac{3}{2}\lambda ,\frac{5}{2}\lambda ,\text{ etc}\text{.)}$, then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths $(\lambda ,2\lambda ,3\lambda ,\text{ etc}\text{.)}$, then constructive interference occurs.

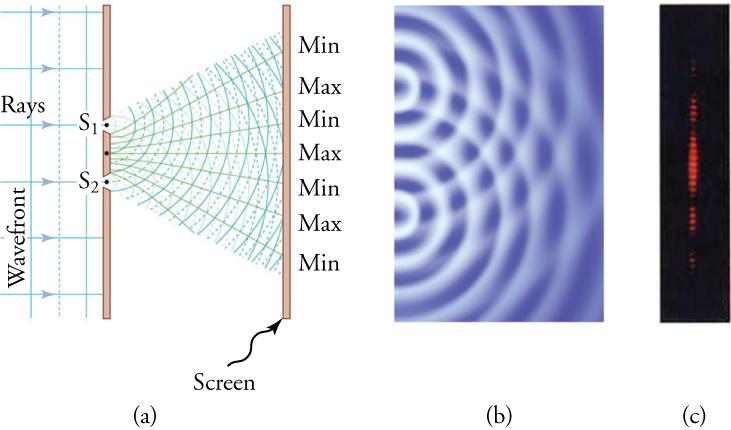
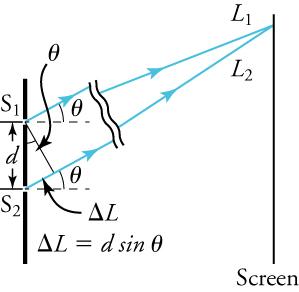
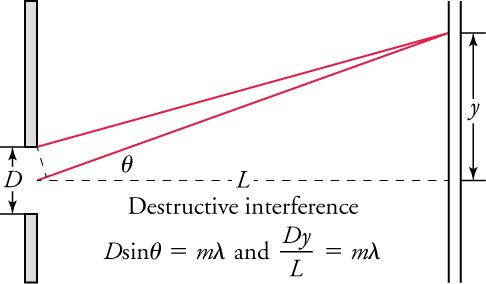
Figure 17.10 shows how to determine the path-length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle $\theta$ between the path and a line from the slits perpendicular to the screen (see the figure) is nearly the same for each path. That approximation and simple trigonometry show the length difference, $\Delta L$, to be $d\sin \theta$, where d is the distance between the slits,

To obtain constructive interference for a double slit, the path-length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit, the path-length difference must be a half-integral multiple of the wavelength, or

The number m is the order of the interference. For example, m = 4 is fourth-order interference.

Figure 17.10 The paths from each slit to a common point on the screen differ by an amount $d\sin \theta$, assuming the distance to the screen is much greater than the distance between the slits (not to scale here).

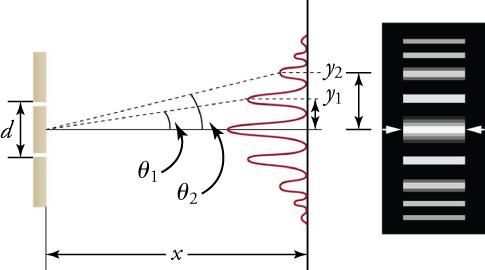
Figure 17.11 shows how the intensity of the bands of constructive interference decreases with increasing angle.

Figure 17.11 The interference pattern for a double slit has an intensity that falls off with angle. The photograph shows multiple bright and dark lines, or fringes, formed by light passing through a double slit.

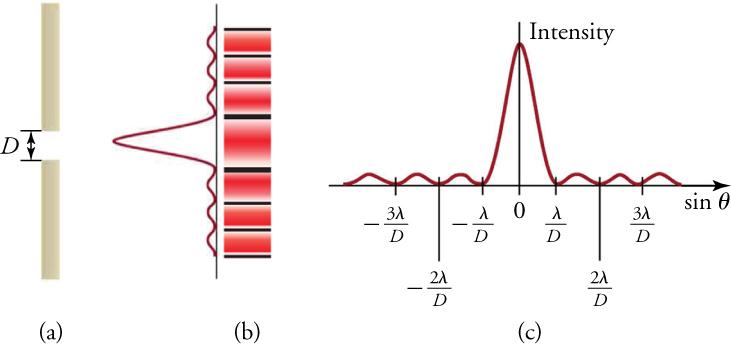
Light passing through a single slit forms a diffraction pattern somewhat different from that formed by double slits. Figure 17.12 shows a single-slit diffraction pattern. Note that the central maximum is larger than those on either side, and that the intensity decreases rapidly on either side.

Figure 17.12 (a) Single-slit diffraction pattern. Monochromatic light passing through a single slit produces a central maximum and many smaller and dimmer maxima on either side. The central maximum is six times higher than shown. (b) The drawing shows the bright central maximum and dimmer and thinner maxima on either side. (c) The location of the minima are shown in terms of $\lambda$ and D.

The analysis of single-slit diffraction is illustrated in Figure 17.13. Assuming the screen is very far away compared with the size of the slit, rays heading toward a common destination are nearly parallel. That approximation allows a series of trigonometric operations that result in the equations for the minima produced by destructive interference.

or

When rays travel straight ahead, they remain in phase and a central maximum is obtained. However, when rays travel at an angle $\theta$ relative to the original direction of the beam, each ray travels a different distance to the screen, and they can arrive in or out of phase. Thus, a ray from the center travels a distance $\lambda /2$ farther than the ray from the top edge of the slit, they arrive out of phase, and they interfere destructively. Similarly, for every ray between the top and the center of the slit, there is a ray between the center and the bottom of the slit that travels a distance $\lambda /2$ farther to the common point on the screen, and so interferes destructively. Symmetrically, there will be another minimum at the same angle below the direct ray.

Figure 17.13 Equations for a single-slit diffraction pattern, where λ is the wavelength of light, D is the slit width, $\theta$ is the angle between a line from the slit to a minimum and a line perpendicular to the screen, L is the distance from the slit to the screen, y is the distance from the center of the pattern to the minimum, and m is a nonzero integer indicating the order of the minimum.

Below we summarize the equations needed for the calculations to follow.

The speed of light in a vacuum, c, the wavelength of the light, $\lambda$, and its frequency, f, are related as follows.

The wavelength of light in a medium, ${\lambda }_n$, compared to its wavelength in a vacuum, $\lambda$, is given by

To calculate the positions of constructive interference for a double slit, the path-length difference must be an integral multiple, m, of the wavelength. $\lambda$

where d is the distance between the slits and $\theta$ is the angle between a line from the slits to the maximum and a line perpendicular to the barrier in which the slits are located. To calculate the positions of destructive interference for a double slit, the path-length difference must be a half-integral multiple of the wavelength:

For a single-slit diffraction pattern, the width of the slit, D, the distance of the first (m = 1) destructive interference minimum, y, the distance from the slit to the screen, L, and the wavelength, $\lambda$, are given by

Also, for single-slit diffraction,

where $\theta$ is the angle between a line from the slit to the minimum and a line perpendicular to the screen, and m is the order of the minimum.