Print Resource

Mysteries of Atomic Spectra

As noted in Quantization of Energy , the energies of some small systems are quantized. Atomic and molecular emission and absorption spectra have been known for over a century to be discrete or quantized (see Figure 13.15). Maxwell and others had realized that there must be a connection between the spectrum of an atom and its structure, something like the resonant frequencies of musical instruments. But, in spite of years of efforts by many great minds, no one had a workable theory. It was a running joke that any theory of atomic and molecular spectra could be destroyed by throwing a book of data at it, so complex were the spectra. Following Einstein’s proposal of photons with quantized energies directly proportional to their wavelengths, it became even more evident that electrons in atoms can exist only in discrete orbits.

Figure 13.15 Part (a) shows, from left to right, a discharge tube, slit, and diffraction grating producing a line spectrum. Part (b) shows the emission line spectrum for iron. The discrete lines imply quantized energy states for the atoms that produce them. The line spectrum for each element is unique, providing a powerful and much used analytical tool, and many line spectra were well known for many years before they could be explained with physics. ((b): Yttrium91, Wikimedia Commons)

In some cases, it had been possible to devise formulas that described the emission spectra. As you might expect, the simplest atom—hydrogen, with its single electron—has a relatively simple spectrum. The hydrogen spectrum had been observed in the infrared (IR), visible, and ultraviolet (UV), and several series of spectral lines had been observed (see Figure 13.16). These series are named after early researchers who studied them in particular depth.

The observed hydrogen-spectrum wavelengths can be calculated using the following formula

where $\lambda$ is the wavelength of the emitted EM radiation and $R$ is the Rydberg constant, determined by the experiment to be

The constant $n_{\text{f}}$ is a positive integer associated with a specific series. For the Lyman series, $n_{\text{f}}=1\text{;}$ for the Balmer series, $n_{\text{f}}=2\text{;}$ for the Paschen series, $n_{\text{f}}=3\text{;}$ and so on. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as $n_{\text{f}}$ increases. The constant $n_{\text{i}}$ is a positive integer, but it must be greater than $n_{\text{f}}\text{.}$ Thus, for the Balmer series, $n_{\text{f}}=2$ and $n_{\text{i}}=\mathrm{3,\; 4,\; 5,\; 6,\; .\; .\; .}\text{.}$ Note that $n_{\text{i}}$ can approach infinity. While the formula in the wavelengths equation was just a recipe designed to fit data and was not based on physical principles, it did imply a deeper meaning. Balmer first devised the formula for his series alone, and it was later found to describe all the other series by using different values of $n_{\text{f.}}$ Bohr was the first to comprehend the deeper meaning. Again, we see the interplay between experiment and theory in physics. Experimentally, the spectra were well established, an equation was found to fit the experimental data, but the theoretical foundation was missing.

Figure 13.16 A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the UV, and the Paschen series and others are in the IR. Values of $n_{\text{f}}$ and $n_{\text{i}}$ are shown for some of the lines.

Bohr’s Solution for Hydrogen

Bohr was able to derive the formula for the hydrogen spectrum using basic physics, the planetary model of the atom, and some very important new proposals. His first proposal is that only certain orbits are allowed: We say that the orbits of electrons in atoms are quantized. Each orbit has a different energy, and electrons can move to a higher orbit by absorbing energy and drop to a lower orbit by emitting energy. If the orbits are quantized, the amount of energy absorbed or emitted is also quantized, producing discrete spectra. Photon absorption and emission are among the primary methods of transferring energy into and out of atoms. The energies of the photons are quantized, and their energy is explained as being equal to the change in energy of the electron when it moves from one orbit to another. In equation form, this is

Here, $\mathrm{\Delta }E$ is the change in energy between the initial and final orbits, and $\text{hf}$ is the energy of the absorbed or emitted photon. It is quite logical, that is, expected from our everyday experience, that energy is involved in changing orbits. A blast of energy is required for the space shuttle, for example, to climb to a higher orbit. What is not expected is that atomic orbits should be quantized. This is not observed for satellites or planets, which can have any orbit given the proper energy (see Figure 13.17).

Figure 13.17 The planetary model of the atom, as modified by Bohr, has the orbits of the electrons quantized. Only certain orbits are allowed, explaining why atomic spectra are discrete—quantized. The energy carried away from an atom by a photon comes from the electron dropping from one allowed orbit to another and is thus quantized. This is likewise true for atomic absorption of photons.

Figure 13.18 shows an energy-level diagram, a convenient way to display energy states. In the present discussion, we take these to be the allowed energy levels of the electron. Energy is plotted vertically with the lowest or ground state at the bottom and with excited states above. Given the energies of the lines in an atomic spectrum, it is possible, although sometimes very difficult, to determine the energy levels of an atom. Energy-level diagrams are used for many systems, including molecules and nuclei. A theory of the atom or any other system must predict its energies based on the physics of the system.

Figure 13.18 An energy-level diagram plots energy vertically and is useful in visualizing the energy states of a system and the transitions between them. This diagram is for the hydrogen-atom electrons, showing a transition between two orbits having energies $E_4$ and $E_2\text{.}$

Bohr was clever enough to find a way to calculate the electron orbital energies in hydrogen. This was an important first step that has been improved upon, but it is well worth repeating here, because it does correctly describe many characteristics of hydrogen. Assuming circular orbits, Bohr proposed that the angular momentum $L$ of an electron in its orbit is quantized, that is, it has only specific, discrete values. The value for $L$ is given by the formula

where $L$ is the angular momentum, $m_e$ is the electron’s mass, $r_n$ is the radius of the $n$th orbit, and $h$ is Planck’s constant. Note that angular momentum is $L=\mathrm{I\omega }\text{.}$ For a small object at a radius $r,I={\text{mr}}^2$ and $\omega =v/r\text{,}$ so that $L=\left({\text{mr}}^2\right)\left(v/r\right)=\text{mvr}\text{.}$ Quantization says that this value of $\text{mvr}$ can only be equal to $h/\mathrm{2,}2h/\mathrm{2,}3h/2\text{,}$ etc. At the time, Bohr himself did not know why angular momentum should be quantized, but using this assumption he was able to calculate the energies in the hydrogen spectrum, something no one else had done at the time.

From Bohr’s assumptions, we will now derive a number of important properties of the hydrogen atom from the classical physics we have covered in the text. We start by noting the centripetal force causing the electron to follow a circular path is supplied by the Coulomb force. To be more general, we note that this analysis is valid for any single-electron atom. So, if a nucleus has $Z$ protons $\text{(}Z=1$ for hydrogen, 2 for helium, etc.) and only one electron, that atom is called a hydrogen-like atom. The spectra of hydrogen-like ions are similar to hydrogen, but shifted to higher energy by the greater attractive force between the electron and nucleus. The magnitude of the centripetal force is $m_e{v}^2/r_n\text{,}$ while the Coulomb force is $k\left({\text{Zq}}_e\right)\left(q_e\right)/r_n^2\text{.}$ The tacit assumption here is that the nucleus is more massive than the stationary electron, and the electron orbits about it. This is consistent with the planetary model of the atom. Equating these

Angular momentum quantization is stated in an earlier equation. We solve that equation for $v\text{,}$ substitute it into the above, and rearrange the expression to obtain the radius of the orbit. This yields

where $a_{\text{B}}$ is defined to be the Bohr radius, since for the lowest orbit $\left(n=1\right)$ and for hydrogen $\left(Z=1\right)\text{,}$ $r_1=a_{\text{B.}}$ It is left for this chapter’s Problems and Exercises to show that the Bohr radius is

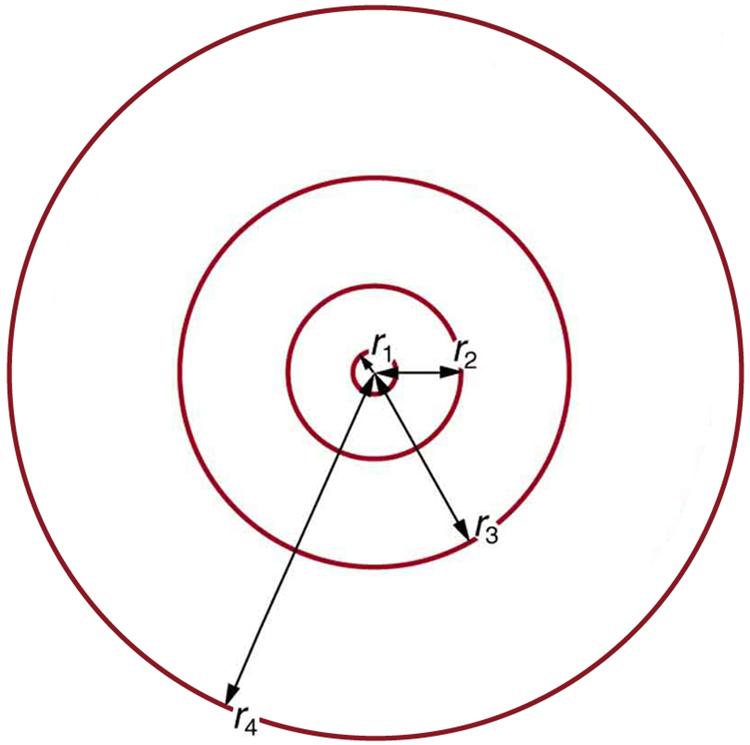
These last two equations can be used to calculate the radii of the allowed (quantized) electron orbits in any hydrogen-like atom. It is impressive that the formula gives the correct size of hydrogen, which is measured experimentally to be very close to the Bohr radius. The earlier equation also tells us that the orbital radius is proportional to $n^2\text{,}$ as illustrated in Figure 13.19.

Figure 13.19 The allowed electron orbits in hydrogen have the radii shown. These radii were first calculated by Bohr and are given by the equation $r_n=\frac{n^2}{Z}{a}_{\text{B}}\text{,}$ The lowest orbit has the experimentally verified diameter of a hydrogen atom.

To get the electron orbital energies, we start by noting that the electron energy is the sum of its kinetic and potential energy

Kinetic energy is the familiar $\text{KE}=\left(1/2\right)m_e{v}^2\text{,}$ assuming the electron is not moving at relativistic speeds. Potential energy for the electron is electrical, or $\text{PE}=q_{e}V\text{,}$ where $V$ is the potential due to the nucleus, which looks like a point charge. The nucleus has a positive charge ${\text{Zq}}_e$; thus, $V={\text{kZq}}_e/r_{n\text{,}}$ recalling an earlier equation for the potential due to a point charge. Since the electron’s charge is negative, we see that $\text{PE}=-{\text{kZq}}_e/r_n\text{,}$ Entering the expressions for $\text{KE}$ and $\text{PE,}$ we find

Now we substitute $r_n$ and $v$ from earlier equations into the above expression for energy. Algebraic manipulation yields

for the orbital energies of hydrogen-like atoms. Here, $E_0$ is the ground-state energy $\left(n=1\right)$ for hydrogen $\left(Z=1\right)$ and is given by

Thus, for hydrogen,

Figure 13.20 shows an energy-level diagram for hydrogen that also illustrates how the various spectral series for hydrogen are related to transitions between energy levels.

Figure 13.20 Energy-level diagram for hydrogen showing the Lyman, Balmer, and Paschen series of transitions. The orbital energies are calculated using the above equation, first derived by Bohr.

Electron total energies are negative, since the electron is bound to the nucleus, analogous to being in a hole without enough kinetic energy to escape. As $n$ approaches infinity, the total energy becomes zero. This corresponds to a free electron with no kinetic energy, since $r_n$ gets very large for large $n\text{,}$ and the electric potential energy thus becomes zero. Thus, 13.6 eV is needed to ionize hydrogen to go from –13.6 eV to 0, or unbound, an experimentally verified number. Given more energy, the electron becomes unbound with some kinetic energy. For example, giving 15.0 eV to an electron in the ground state of hydrogen strips it from the atom and leaves it with 1.4 eV of kinetic energy.

Finally, let us consider the energy of a photon emitted in a downward transition, given by the equation to be

Substituting $E_n=(–\text{13.6 eV}/n^2)\text{,}$ we see that

Dividing both sides of this equation by $\text{hc}$ gives an expression for $1/\lambda$

It can be shown that

is the Rydberg constant. Thus, we have used Bohr’s assumptions to derive the formula first proposed by Balmer years earlier as a recipe to fit experimental data.

We see that Bohr’s theory of the hydrogen atom answers the question as to why this previously known formula describes the hydrogen spectrum. It is because the energy levels are proportional to $1/n^2\text{,}$ where $n$ is a non-negative integer. A downward transition releases energy, and so $n_{\mathrm{i}}$ must be greater than $n_{\text{f}}\text{.}$ The various series are those where the transitions end on a certain level. For the Lyman series, $n_{\text{f}}=1$—that is, all the transitions end in the ground state (see also Figure 13.20). For the Balmer series, $n_{\text{f}}=2\text{,}$ or all the transitions end in the first excited state and so on. What was once a recipe is now based in physics, and something new is emerging—angular momentum is quantized.

Triumphs and Limits of the Bohr Theory

Bohr did what no one had been able to do before. Not only did he explain the spectrum of hydrogen, he correctly calculated the size of the atom from basic physics. Some of his ideas are broadly applicable. Electron orbital energies are quantized in all atoms and molecules. Angular momentum is quantized. The electrons do not spiral into the nucleus, as expected classically—accelerated charges radiate, so that the electron orbits classically would decay quickly, and the electrons would sit on the nucleus—matter would collapse. These are major triumphs.

But there are limits to Bohr’s theory. It cannot be applied to multielectron atoms, even one as simple as a two-electron helium atom. Bohr’s model is what we call semiclassical. The orbits are quantized—nonclassical—but are assumed to be simple circular paths—classical. As quantum mechanics was developed, it became clear that there are no well-defined orbits; rather, there are clouds of probability. Bohr’s theory also did not explain that some spectral lines are doublets—split into two—when examined closely. We shall examine many of these aspects of quantum mechanics in more detail, but it should be kept in mind that Bohr did not fail. Rather, he made very important steps along the path to greater knowledge and laid the foundation for all of atomic physics that has since evolved.