Print Resource

Rutherford’s Experiment

In the early 1900’s, the plum pudding model was the accepted model of the atom. Proposed in 1904 by J. J. Thomson, the model suggested that the atom was a spherical ball of positive charge, with negatively charged electrons scattered evenly throughout. In that model, the positive charges made up the pudding, while the electrons acted as isolated plums. During its short life, the model could be used to explain why most particles were neutral, although with an unbalanced number of plums, electrically charged atoms could exist.

When Ernest Rutherford began his gold foil experiment in 1909, it is unlikely that anyone would have expected that the plum pudding model would be challenged. However, using a radioactive source, a thin sheet of gold foil, and a phosphorescent screen, Rutherford would uncover something so great that he would later call it “the most incredible event that has ever happened to me in my life”[James, L. K. (1993). Nobel Laureates in Chemistry, 1901–1992. Washington, DC: American Chemical Society.]

The experiment that Rutherford designed is shown in Figure 22.2. As you can see in, a radioactive source was placed in a lead container with a hole in one side to produce a beam of positively charged helium particles, called alpha particles. Then, a thin gold foil sheet was placed in the beam. When the high-energy alpha particles passed through the gold foil, they were scattered. The scattering was observed from the bright spots they produced when they struck the phosphor screen.

Figure 22.2 Rutherford’s experiment gave direct evidence for the size and mass of the nucleus by scattering alpha particles from a thin gold foil. The scattering of particles suggests that the gold nuclei are very small and contain nearly all of the gold atom’s mass. Particularly significant in showing the size of the nucleus are alpha particles that scatter to very large angles, much like a soccer ball bouncing off a goalie’s head.

The expectation of the plum pudding model was that the high-energy alpha particles would be scattered only slightly by the presence of the gold sheet. Because the energy of the alpha particles was much higher than those typically associated with atoms, the alpha particles should have passed through the thin foil much like a supersonic bowling ball would crash through a few dozen rows of bowling pins. Any deflection was expected to be minor, and due primarily to the electrostatic Coulomb force between the alpha particles and the foil’s interior electric charges.

However, the true result was nothing of the sort. While the majority of alpha particles passed through the foil unobstructed, Rutherford and his collaborators Hans Geiger and Ernest Marsden found that alpha particles occasionally were scattered to large angles, and some even came back in the direction from which they came! The result, called Rutherford scattering, implied that the gold nuclei were actually very small when compared with the size of the gold atom. As shown in Figure 22.3, the dense nucleus is surrounded by mostly empty space of the atom, an idea verified by the fact that only 1 in 8,000 particles was scattered backward.

Figure 22.3 An expanded view of the atoms in the gold foil in Rutherford’s experiment. Circles represent the atoms that are about 10⁻¹⁰ m in diameter, while the dots represent the nuclei that are about 10⁻¹⁵ m in diameter. To be visible, the dots are much larger than scale—if the nuclei were actually the size of the dots, each atom would have a diameter of about five meters! Most alpha particles crash through but are relatively unaffected because of their high energy and the electron’s small mass. Some, however, strike a nucleus and are scattered straight back. A detailed analysis of their interaction gives the size and mass of the nucleus.

Although the results of the experiment were published by his colleagues in 1909, it took Rutherford two years to convince himself of their meaning. Rutherford later wrote: “It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration, I realized that this scattering backwards ... [meant] ... the greatest part of the mass of the atom was concentrated in a tiny nucleus.” In 1911, Rutherford published his analysis together with a proposed model of the atom, which was in part based on Geiger’s work from the previous year. As a result of the paper, the size of the nucleus was determined to be about ${10}^{\mathrm{-15}}$ m, or 100,000 times smaller than the atom. That implies a huge density, on the order of ${10}^{15}$ g/cm³, much greater than any macroscopic matter.

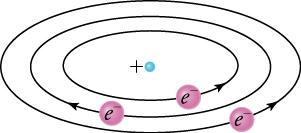
Based on the size and mass of the nucleus revealed by his experiment, as well as the mass of electrons, Rutherford proposed the planetary model of the atom. The planetary model of the atom pictures low-mass electrons orbiting a large-mass nucleus. The sizes of the electron orbits are large compared with the size of the nucleus, and most of the atom is a vacuum. The model is analogous to how low-mass planets in our solar system orbit the large-mass Sun. In the atom, the attractive Coulomb force is analogous to gravitation in the planetary system (see Figure 22.4).

Figure 22.4 Rutherford’s planetary model of the atom incorporates the characteristics of the nucleus, electrons, and the size of the atom. The model was the first to recognize the structure of atoms, in which low-mass electrons orbit a very small, massive nucleus in orbits much larger than the nucleus. The atom is mostly empty and is analogous to our planetary system.

Virtual Physics

Rutherford Scattering

Figure 22.5 Click here for the Rutherford Scattering simulation.

How did Rutherford figure out the structure of the atom without being able to see it? Explore the answer through this simulation of the famous experiment in which he disproved the plum pudding model by observing alpha particles bouncing off atoms and determining that they must have a small core.

Absorption and Emission Spectra

In 1900, Max Planck recognized that all energy radiated from a source is emitted by atoms in quantum states. How would that radical idea relate to the interior of an atom? The answer was first found by investigating the spectrum of light or emission spectrum produced when a gas is highly energized.

Figure 22.6 shows how to isolate the emission spectrum of one such gas. The gas is placed in the discharge tube at the left, where it is energized to the point at which it begins to radiate energy or emit light. The radiated light is channeled by a thin slit and then passed through a diffraction grating, which will separate the light into its constituent wavelengths. The separated light will then strike the photographic film on the right.

The line spectrum shown in part (b) of Figure 22.6 is the output shown on the film for excited iron. Note that this spectrum is not continuous but discrete. In other words, only particular wavelengths are emitted by the iron source. Why would that be the case?

Figure 22.6 Part (a) shows, from left to right, a discharge tube, slit, and diffraction grating producing a line spectrum. Part (b) shows the emission spectrum for iron. The discrete lines imply quantized energy states for the atoms that produce them. The line spectrum for each element is unique, providing a powerful and much-used analytical tool, and many line spectra were well known for many years before they could be explained with physics. (credit:(b) Yttrium91, Wikimedia Commons)

The spectrum of light created by excited iron shows a variety of discrete wavelengths emitted within the visible spectrum. Each element, when excited to the appropriate degree, will create a discrete emission spectrum as in part (b) of Figure 22.6. However, the wavelengths emitted will vary from element to element. The emission spectrum for iron was chosen for Figure 22.6 solely because a substantial portion of its emission spectrum is within the visible spectrum. Figure 22.7 shows the emission spectrum for hydrogen. Note that, while discrete, a large portion of hydrogen emission takes place in the ultraviolet and infrared regions.

Figure 22.7 A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the ultraviolet, and the Paschen series and others are in the infrared. Values of n_f and n_i are shown for some of the lines. Their importance will be described shortly.

Just as an emission spectrum shows all discrete wavelengths emitted by a gas, an absorption spectrum will show all light that is absorbed by a gas. Black lines exist where the wavelengths are absorbed, with the remainder of the spectrum lit by light is free to pass through. What relationship do you think exists between the black lines of a gas’s absorption spectrum and the colored lines of its emission spectrum? Figure 22.8 shows the absorption spectrum of the Sun. The black lines are called Fraunhofer lines, and they correspond to the wavelengths absorbed by gases in the Sun’s exterior.

Figure 22.8 The absorption spectrum of the Sun. The black lines appear at wavelengths absorbed by the Sun’s gas exterior. The energetic photons emitted from the Sun’s interior are absorbed by gas in its exterior and reemitted in directions away from the observer. That results in dark lines within the absorption spectrum. The lines are called Fraunhofer lines, in honor of the German physicist who discovered them. Lines similar to those are used to determine the chemical composition of stars well outside our solar system.

Bohr’s Explanation of the Hydrogen Spectrum

To tie the unique signatures of emission spectra to the composition of the atom itself would require clever thinking. Niels Bohr (1885–1962), a Danish physicist, did just that, by making immediate use of Rutherford’s planetary model of the atom. Bohr, shown in Figure 22.9, became convinced of its validity and spent part of 1912 at Rutherford’s laboratory. In 1913, after returning to Copenhagen, he began publishing his theory of the simplest atom, hydrogen, based on Rutherford’s planetary model.

Figure 22.9 Niels Bohr, Danish physicist, used the planetary model of the atom to explain the atomic spectrum and size of the hydrogen atom. His many contributions to the development of atomic physics and quantum mechanics, his personal influence on many students and colleagues, and his personal integrity, especially in the face of Nazi oppression, earned him a prominent place in history. (credit: Unknown Author, Wikimedia Commons)

Bohr was able to derive the formula for the hydrogen spectrum using basic physics, the planetary model of the atom, and some very important new conjectures. His first conjecture was that only certain orbits are allowed: In other words, in an atom, the orbits of electrons are quantized. Each quantized orbit has a different distinct energy, and electrons can move to a higher orbit by absorbing energy or drop to a lower orbit by emitting energy. Because of the quantized orbits, the amount of energy emitted or absorbed must also be quantized, producing the discrete spectra seen in Figure 22.6 and Figure 22.8. In equation form, the amount of energy absorbed or emitted can be found as

where $E_i$ refers to the energy of the initial quantized orbit, and $E_f$ refers to the energy of the final orbits. Furthermore, the wavelength emitted can be found using the equation

and relating the wavelength to the frequency found using the equation $v=f\lambda$, where v corresponds to the speed of light.

It makes sense that energy is involved in changing orbits. For example, a burst of energy is required for a satellite to climb to a higher orbit. What is not expected is that atomic orbits should be quantized. Quantization is not observed for satellites or planets, which can have any orbit, given the proper energy (see Figure 22.10).

Figure 22.10 The planetary model of the atom, as modified by Bohr, has the orbits of the electrons quantized. Only certain orbits are allowed, explaining why atomic spectra are discrete or quantized. The energy carried away from an atom by a photon comes from the electron dropping from one allowed orbit to another and is thus quantized. The same is true for atomic absorption of photons.

Figure 22.11 shows an energy-level diagram, a convenient way to display energy states. Each of the horizontal lines corresponds to the energy of an electron in a different orbital. Energy is plotted vertically with the lowest or ground state at the bottom and with excited states above. The vertical arrow downwards shows energy being emitted out of the atom due to an electron dropping from one excited state to another. That would correspond to a line shown on the atom’s emission spectrum. The Lyman series shown in Figure 22.7 results from electrons dropping to the ground state, while the Balmer and Paschen series result to electrons dropping to the n = 2 and n = 3 states, respectively.

Figure 22.11 An energy-level diagram plots energy vertically and is useful in visualizing the energy states of a system and the transitions between them. This diagram is for the hydrogen-atom electrons, showing a transition between two orbits having energies $E_4$ and $E_2$. The energy transition results in a Balmer series line in an emission spectrum.

Energy and Wavelength of Emitted Hydrogen Spectra

The energy associated with a particular orbital of a hydrogen atom can be found using the equation

where n corresponds to the orbital value from the atom’s nucleus. The negative value in the equation is based upon a baseline energy of zero when the electron is infinitely far from the atom. As a result, the negative value shows that energy is necessary to free the electron from its orbital state. The minimum energy to free the electron is also referred to as its binding energy. The equation is only valid for atoms with single electrons in their orbital shells (like hydrogen). For ionized atoms similar to hydrogen, the following formula may be used.

Please note that $E_o$ corresponds to –13.6 eV, as mentioned earlier. Additionally, $Z$ refers to the atomic number of the element studied. The atomic number is the number of protons in the nucleus—it is different for each element. The above equation is derived from some basic physics principles, namely conservation of energy, conservation of angular momentum, Coulomb’s law, and centripetal force. There are three derivations that result in the orbital energy equations, and they are shown below. While you can use the energy equations without understanding the derivations, they will help to remind you of just how valuable those fundamental concepts are.

Derivation 3 (Finding the Energy of the Orbiting Electron)

To get the electron orbital energies, we start by noting that the electron energy is the sum of its kinetic and potential energy.

22.8$$E_n=KE+PE$$

Kinetic energy is the familiar $KE=\frac{1}{2}m{v}^2$, assuming the electron is not moving at a relativistic speed. Potential energy for the electron is electrical, or $PE=q_{e}V$, where V is the potential due to the nucleus, which looks like a point charge. The nucleus has a positive charge $Z{q}_e$; thus, $V=\frac{kZ{q}_e}{r_n}$, recalling an earlier equation for the potential due to a point charge from the chapter on Electricity and Magnetism. Since the electron’s charge is negative, we see that $PE=\frac{-kZ{q}_e{}^2}{r_n}\text{.}$Substituting the expressions for KE and PE,

22.9$$E_n=\frac{1}{2}{m}_e{v}^2-\frac{kZ{q}_e{}^2}{r_n}.$$

Now we solve for r_n and v using the equation for angular momentum $L=m_{e}v{r}_n=n\frac{h}{2\pi }(n=1,2,3,\mathrm{...})$, giving

22.10$$v=n\frac{h}{2\pi m_e{r}_n}(n=1,2,3,\mathrm{...})$$

and

22.11$$r_n=n\frac{h}{2\pi m_{e}v}(n=1,2,3,\mathrm{...}).$$

Substituting the expression for r_n and v into the above expressions for energy (KE and PE), and performing algebraic manipulation, yields

22.12$$E_n=-\frac{Z^2}{n^2}{E}_o(n=1,2,3,\mathrm{...})$$

for the orbital energies of hydrogen-like atoms. Here, E_o is the ground-state energy (n = 1) for hydrogen (Z = 1) and is given by

22.13$$E_o=\frac{2{\pi }^2{q}_e{}^4{m}_e{k}^2}{h^2}=13.6\text{eV}\text{.}$$

Thus, for hydrogen,

22.14$$E_n=-\frac{13.6\text{eV}}{n^2}(n=1,2,3,\mathrm{...}).$$

The relationship between orbital energies and orbital states for the hydrogen atom can be seen in Figure 22.12.

Figure 22.12 Energy-level diagram for hydrogen showing the Lyman, Balmer, and Paschen series of transitions. The orbital energies are calculated using the above equation, first derived by Bohr.

Worked Example

A hydrogen atom is struck by a photon. How much energy must be absorbed from the photon to raise the electron of the hydrogen atom from its ground state to its second orbital?

Strategy

The hydrogen atom has an atomic number of Z = 1. Raising the electron from the ground state to its second orbital will increase its orbital level from n = 1 to n = 2. The energy determined will be measured in electron-volts.

Solution

The amount of energy necessary to cause the change in electron state is the difference between the final and initial energies of the electron. The final energy state of the electron can be found using

22.15$$E_n=\frac{Z^2}{n^2}{E}_o\left(n=1,2,3,\mathrm{...}\right)\text{.}$$

Knowing the n and Z values for the hydrogen atom, and knowing that E_o = –13.6 eV, the result is

22.16$$E_f=\frac{1^2}{2^2}(-13.6\text{eV})=-3.4\text{eV}.$$

The original amount of energy associated with the electron is equivalent to the ground state orbital, or

22.17$$E_O=\frac{1^2}{1^2}(-13.6\text{eV})=\mathrm{-13.6}\text{eV}.$$

The amount of energy necessary to change the orbital state of the electron can be found by determining the electron’s change in energy.

22.18$$\text{Δ}E=E_f-E_o=\left(-3.4\text{e}\text{V}\right)-\left(-13.6\text{e}\text{V}\right)=+10.2\text{e}\text{V}$$

Discussion

The energy required to change the orbital state of the electron is positive. That means that for the electron to move to a state with greater energy, energy must be added to the atom. Should the electron drop back down to its original energy state, a change of –10.2 eV would take place, and 10.2 eV of energy would be emitted from the atom. Just as only quantum amounts of energy may be absorbed by the atom, only quantum amounts of energy can be emitted from the atom. That helps to explain many of the quantum light effects that you have learned about previously.

Worked Example

Characteristic X-Ray Energy

Calculate the approximate energy of an X-ray emitted for an n = 2 to n = 1 transition in a tungsten anode in an X-ray tube.

Strategy

How do we calculate energies in a multiple-electron atom? In the case of characteristic X-rays, the following approximate calculation is reasonable. Characteristic X-rays are produced when an inner-shell vacancy is filled. Inner-shell electrons are nearer the nucleus than others in an atom and thus feel little net effect from the others. That is similar to what happens inside a charged conductor, where its excess charge is distributed over the surface so that it produces no electric field inside. It is reasonable to assume the inner-shell electrons have hydrogen-like energies, as given by

22.19$$E_n=\frac{Z^2}{n^2}{E}_o\left(n=1,2,3,\mathrm{...}\right)$$

For tungsten, Z = 74, so that the effective charge is 73.

Solution

The amount of energy given off as an X-ray is found using

22.20$$\text{Δ}E=hf=E_i-E_f,$$

where

22.21$$E_f=-\frac{Z^2}{1^2}{E}_o=-\frac{{73}^2}{1}\left(13.6\text{e}\text{V}\right)=-72.5\text{k}\text{e}\text{V}$$

and

22.22$$E_i=-\frac{Z^2}{2^2}{E}_o=-\frac{{73}^2}{4}(13.6\text{eV})=\mathrm{-18.1}\text{keV}.$$

Thus,

22.23$$\text{Δ}E=E_i-E_f=\left(\mathrm{-18.1}\text{k}\text{e}\text{V}\right)-\left(\mathrm{-72.5}\text{k}\text{e}\text{V}\right)=54.4\text{k}\text{e}\text{V}.$$

Discussion

This large photon energy is typical of characteristic X-rays from heavy elements. It is large compared with other atomic emissions because it is produced when an inner-shell vacancy is filled, and inner-shell electrons are tightly bound. Characteristic X-ray energies become progressively larger for heavier elements because their energy increases approximately as Z². Significant accelerating voltage is needed to create such inner-shell vacancies, because other shells are filled and you cannot simply bump one electron to a higher filled shell. You must remove it from the atom completely. In the case of tungsten, at least 72.5 kV is needed. Tungsten is a common anode material in X-ray tubes; so much of the energy of the impinging electrons is absorbed, raising its temperature, that a high-melting-point material like tungsten is required.

The wavelength of light emitted by an atom can also be determined through basic derivations. Let us consider the energy of a photon emitted from a hydrogen atom in a downward transition, given by the equation

22.24$$\text{Δ}E=hf=E_i-E_f$$

Substituting $E_n=\left(\frac{\mathrm{-13.6}\text{e}\text{V}}{n^2}\right)$ , we get

22.25$$hf=\left(13.6\text{e}\text{V}\right)(\frac{1}{n_f{}^2}-\frac{1}{n_i{}^2}).$$

Dividing both sides of the equation by hc gives us an expression for $\frac{1}{\lambda }$,

22.26$$\frac{hf}{hc}=\frac{f}{c}=\frac{1}{\lambda }=\frac{13.6\text{eV}}{hc}(\frac{1}{n_f{}^2}-\frac{1}{n_i{}^2}).$$

It can be shown that

22.27$$\left(\frac{13.6\text{eV}}{hc}\right)=\frac{(13.6\text{eV})(1.602\times {10}^{\mathrm{-19}}\text{J}/\text{eV})}{(6.602\times {10}^{\mathrm{-34}}\text{J}\cdot \text{s})(2.998\times {10}^8\text{m}/\text{s})}=1.097\times {10}^7{\text{m}}^{\mathrm{-1}}=R,$$

where R is the Rydberg constant.

Simplified, the formula for determining emitted wavelength can now be written as

22.28$$\frac{1}{\lambda }=R(\frac{1}{n_f{}^2}-\frac{1}{n_i{}^2}).$$

Worked Example

 

What wavelength of light is emitted by an electron dropping from the third orbital to the ground state of a hydrogen atom?

Strategy

The ground state of a hydrogen atom is considered the first orbital of the atom. As a result, n_f = 1 and n_i = 3. The Rydberg constant has already been determined and will be constant regardless of atom chosen.

Solution

22.29 $$\frac{1}{\lambda }=R\left(\frac{1}{n_f{}^2}-\frac{1}{n_i{}^2}\right)$$

For the equation above, calculate wavelength based on the known energy states.

22.30$$\frac{1}{\lambda }=1.097\times {10}^7\left(\frac{1}{1^2}-\frac{1}{3^2}\right)=9.751\times {10}^6{\text{m}}^{\mathrm{-1}}$$

Rearranging the equation for wavelength yields

22.31$$\lambda =1.026\times {10}^{\mathrm{-7}}\text{m}=102.6\text{nm}.$$

Discussion

This wavelength corresponds to light in the ultraviolet spectrum. As a result, we would not be able to see the photon of light emitted when an electron drops from its third to first energy state. However, it is worth noting that by supplying light of wavelength precisely 102.6 nm, we can cause the electron in hydrogen to move from its first to its third orbital state.

Limits of Bohr’s Theory and the Quantum Model of the Atom

There are limits to Bohr’s theory. It does not account for the interaction of bound electrons, so it cannot be fully applied to multielectron atoms, even one as simple as the two-electron helium atom. Bohr’s model is what we call semiclassical. The orbits are quantized (nonclassical) but are assumed to be simple circular paths (classical). As quantum mechanics was developed, it became clear that there are no well-defined orbits; rather, there are clouds of probability. Additionally, Bohr’s theory did not explain that some spectral lines are doublets or split into two when examined closely. While we shall examine a few of those aspects of quantum mechanics in more detail, it should be kept in mind that Bohr did not fail. Rather, he made very important steps along the path to greater knowledge and laid the foundation for all of atomic physics that has since evolved.

DeBroglie’s Waves

Following Bohr’s initial work on the hydrogen atom, a decade was to pass before Louis de Broglie proposed that matter has wave properties. The wave-like properties of matter were subsequently confirmed by observations of electron interference when scattered from crystals. Electrons can exist only in locations where they interfere constructively. How does that affect electrons in atomic orbits? When an electron is bound to an atom, its wavelength must fit into a small space, something like a standing wave on a string (see Figure 22.13). Orbits in which an electron can constructively interfere with itself are allowed. All orbits in which constructive interference cannot occur are not able to exist. Thus, only certain orbits are allowed. The wave nature of an electron, according to de Broglie, is why the orbits are quantized!

Figure 22.13 (a) Standing waves on a string have a wavelength related to the length of the string, allowing them to interfere constructively. (b) If we imagine the string formed into a closed circle, we get a rough idea of how electrons in circular orbits can interfere constructively. (c) If the wavelength does not fit into the circumference, the electron interferes destructively; it cannot exist in such an orbit.

For a circular orbit, constructive interference occurs when the electron’s wavelength fits neatly into the circumference, so that wave crests always align with crests and wave troughs align with troughs, as shown in Figure 22.13(b). More precisely, when an integral multiple of the electron’s wavelength equals the circumference of the orbit, constructive interference is obtained. In equation form, the condition for constructive interference and an allowed electron orbit is

22.32$$n{\lambda }_n=2\pi r_n(n=1,2,3,\mathrm{...}),$$

where ${\lambda }_n$ is the electron’s wavelength and r_n is the radius of that circular orbit. Figure 22.14 shows the third and fourth orbitals of a hydrogen atom.

Figure 22.14 The third and fourth allowed circular orbits have three and four wavelengths, respectively, in their circumferences.

Heisenberg Uncertainty

How does determining the location of an electron change its trajectory? The answer is fundamentally important—measurement affects the system being observed. It is impossible to measure a physical quantity exactly, and greater precision in measuring one quantity produces less precision in measuring a related quantity. It was Werner Heisenberg who first stated that limit to knowledge in 1929 as a result of his work on quantum mechanics and the wave characteristics of all particles (see Figure 22.15).

Figure 22.15 Werner Heisenberg was the physicist who developed the first version of true quantum mechanics. Not only did his work give a description of nature on the very small scale, it also changed our view of the availability of knowledge. Although he is universally recognized for the importance of his work by receiving the Nobel Prize in 1932, for example, Heisenberg remained in Germany during World War II and headed the German effort to build a nuclear bomb, permanently alienating himself from most of the scientific community. (credit: Unknown Author, Wikimedia Commons)

For example, you can measure the position of a moving electron by scattering light or other electrons from it. However, by doing so, you are giving the electron energy, and therefore imparting momentum to it. As a result, the momentum of the electron is affected and cannot be determined precisely. This change in momentum could be anywhere from close to zero up to the relative momentum of the electron ($p\approx h/\lambda$). Note that, in this case, the particle is an electron, but the principle applies to any particle.

Viewing the electron through the model of wave-particle duality, Heisenberg recognized that, because a wave is not located at one fixed point in space, there is an uncertainty associated with any electron’s position. That uncertainty in position, $\text{Δ}x$, is approximately equal to the wavelength of the particle. That is, $\text{Δ}x\approx \lambda$. There is an interesting trade-off between position and momentum. The uncertainty in an electron’s position can be reduced by using a shorter-wavelength electron, since $\text{Δ}x\approx \lambda$. But shortening the wavelength increases the uncertainty in momentum, since $\text{Δ}p\approx h/\lambda$. Conversely, the uncertainty in momentum can be reduced by using a longer-wavelength electron, but that increases the uncertainty in position. Mathematically, you can express the trade-off by multiplying the uncertainties. The wavelength cancels, leaving

$$\text{Δ}x\text{Δ}p\approx h.$$

Therefore, if one uncertainty is reduced, the other must increase so that their product is $\approx h$ . With the use of advanced mathematics, Heisenberg showed that the best that can be done in a simultaneous measurement of position and momentum is

22.33$$\text{Δ}x\text{Δ}p\ge \frac{h}{4\pi }.$$

That relationship is known as the Heisenberg uncertainty principle.

The Quantum Model of the Atom

Because of the wave characteristic of matter, the idea of well-defined orbits gives way to a model in which there is a cloud of probability, consistent with Heisenberg’s uncertainty principle. Figure 22.16 shows how the principle applies to the ground state of hydrogen. If you try to follow the electron in some well-defined orbit using a probe that has a wavelength small enough to measure position accurately, you will instead knock the electron out of its orbit. Each measurement of the electron’s position will find it to be in a definite location somewhere near the nucleus. Repeated measurements reveal a cloud of probability like that in the figure, with each speck the location determined by a single measurement. There is not a well-defined, circular-orbit type of distribution. Nature again proves to be different on a small scale than on a macroscopic scale.

Figure 22.16 The ground state of a hydrogen atom has a probability cloud describing the position of its electron. The probability of finding the electron is proportional to the darkness of the cloud. The electron can be closer or farther than the Bohr radius, but it is very unlikely to be a great distance from the nucleus.

Virtual Physics

Models of the Hydrogen Atom

Figure 22.17 Click here for the Models of the Hydrogen Atom simulation.

How did scientists figure out the structure of atoms without looking at them? Try out different models by shooting light at the atom. Use this simulation to see how the prediction of the model matches the experimental results.