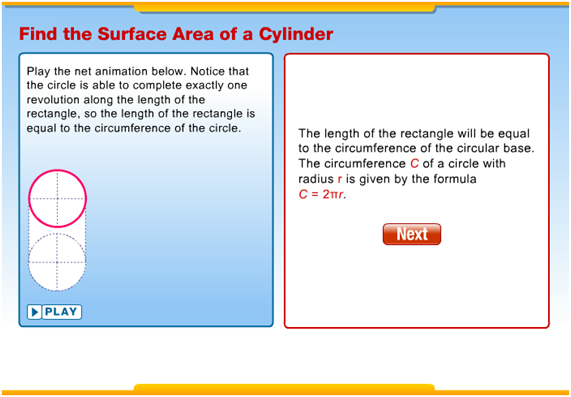
Introduction
 3-dimensional figures occur everywhere in the world around us, especially in fields such as architecture.
3-dimensional figures occur everywhere in the world around us, especially in fields such as architecture.
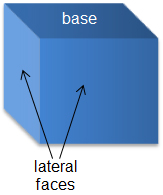
A prism is a 3-dimensional figure that has two parallel, congruent bases connected by lateral faces. The lateral faces of a prism are always parallelograms and are usually rectangles. A prism is named by the shape of its base. So, a prism with a rectangular-shaped base is called a rectangular prism. Likewise, a prism with a hexagonal-shaped base is called a hexagonal prism.
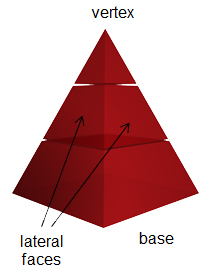 A pyramid is a 3-dimensional figure that has one base. The lateral faces of a pyramid are triangles that meet at one point, which is called the vertex. Like prisms, pyramids are named by the shape of their base. A pyramid with a square base is called a square pyramid.
A pyramid is a 3-dimensional figure that has one base. The lateral faces of a pyramid are triangles that meet at one point, which is called the vertex. Like prisms, pyramids are named by the shape of their base. A pyramid with a square base is called a square pyramid.
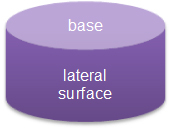
A cylinder is like a prism, but the bases of a cylinder are circles instead of polygons. A cylinder has two circular bases and a curved lateral surface. Since the surfaces of a cylinder are not polygons (they have round edges and are not always planar figures), we call them surfaces instead of faces.

Consider the barn and silo shown. The silo is in the shape of a cylinder with a half-dome roof. The barn is a prism with a seven-sided polygon as the base, so we can call the barn a heptagonal prism.
Introducing Nets
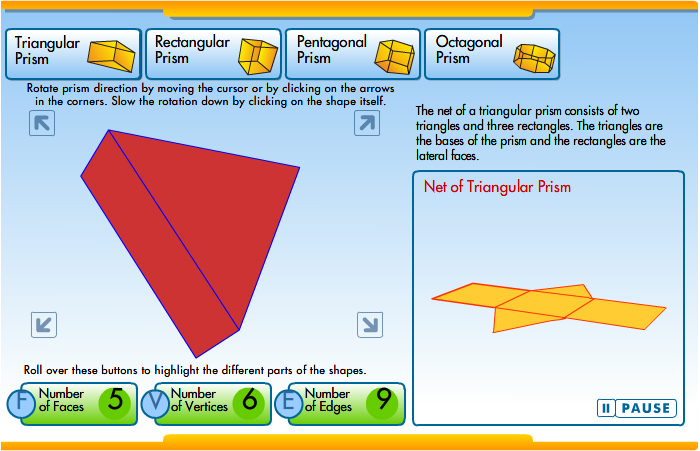
A net is a 2-dimensional representation of a 3-dimensional figure. A net is a flat figure that could be folded to create the 3-dimensional figure. Engineers and draftsmen frequently use nets to represent 3-dimensional figures, since a net can be stamped into metal or cut out of paper and folded to create a 3-dimensional figure.
Click on the image below, and use the interactive to see how different nets can be folded to create different types of prisms. Be sure to view triangular, rectangular, pentagonal, and octagonal prisms.
Need additional directions?
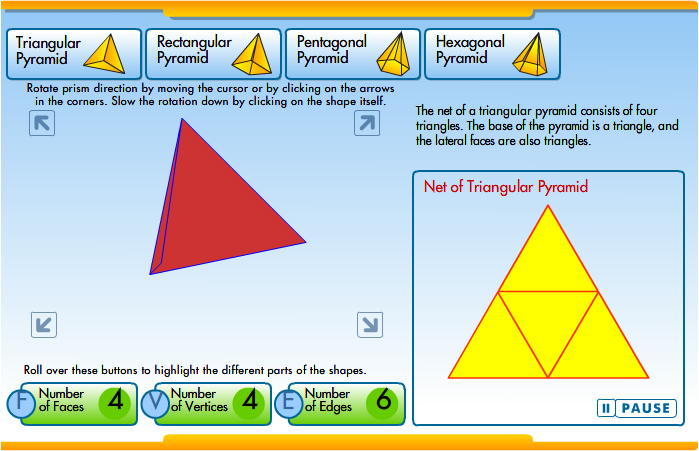
Click on the image below, and use the interactive to see how different nets can be folded to create different types of pyramids. Be sure to view triangular, rectangular, pentagonal, and hexagonal pyramids.
Need additional directions?
Determining Lateral Surface Area
When working with actual 3-dimensional solids, the lateral surface (or surfaces) is oftentimes important in its own right.
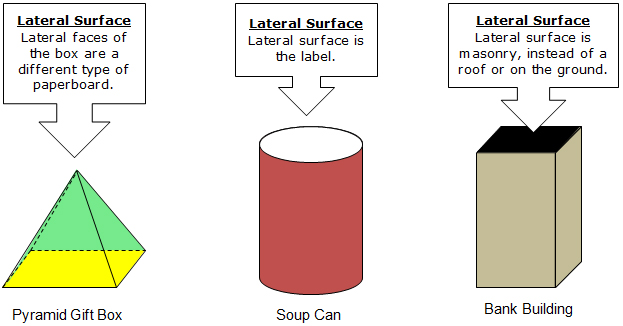
In these cases, and many others, it is important to be able to determine the area of only the lateral surface or lateral faces. That area is called the lateral surface area.
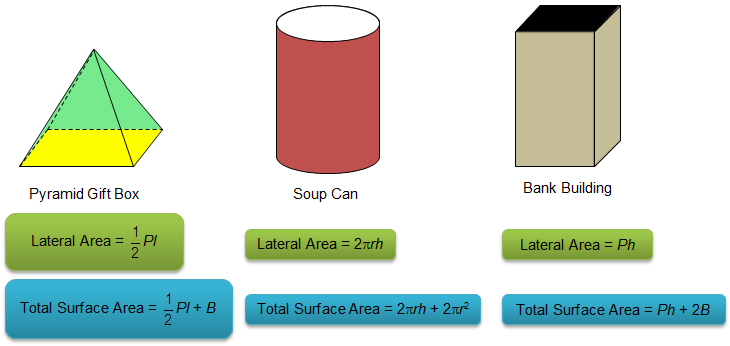
Let’s unfold the pyramid gift box to create its net.
Use the dimensions provided to calculate the area of each of the lateral faces of the pyramid. Then calculate the lateral surface area of the pyramid by finding the sum of areas of the lateral faces.
Let's unfold the soup can to create its net.
Let's unfold the bank building to create its net.
Practice
For each of the nets below, calculate the lateral surface area. Use 3.14 for π.
Cylinder:
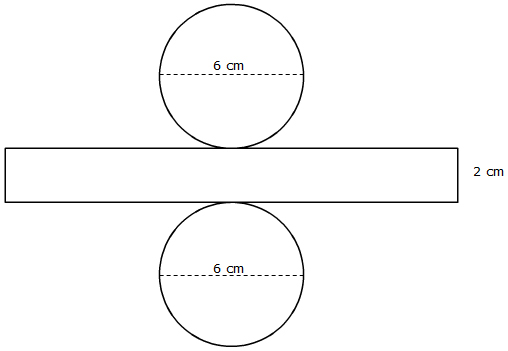
Square Pyramid:
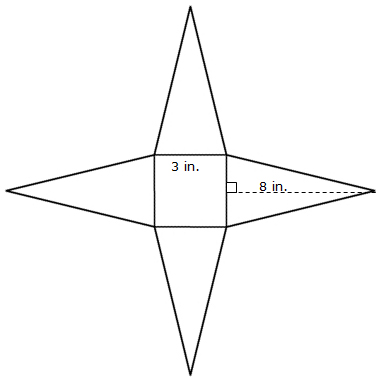
Triangular Prism:
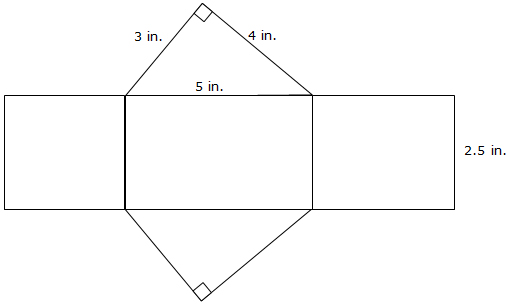
Determining Total Surface Area
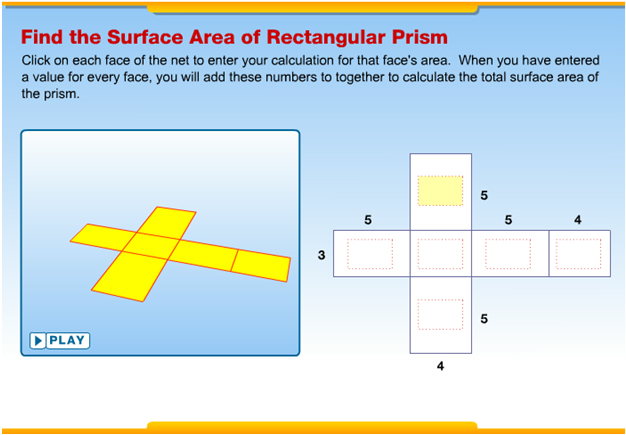
Click on the image below to access the interactive. Follow the directions on how to use a net to determine the total surface area of a rectangular prism.
Click on the image below to access the interactive. Follow the directions on how to use a net to determine the total surface area of a cylinder.
Practice
For each of the nets below, calculate the total surface area. Use 3.14 for π.
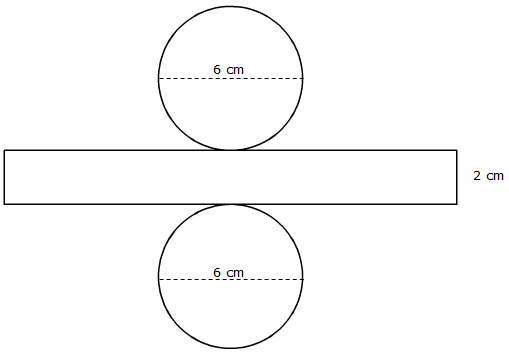
Cylinder
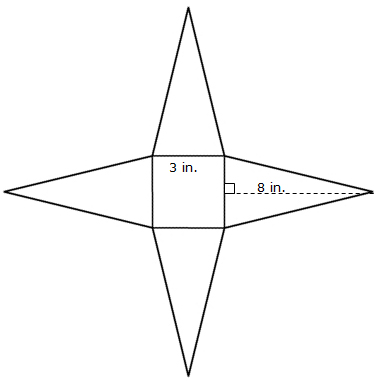
Square Pyramid
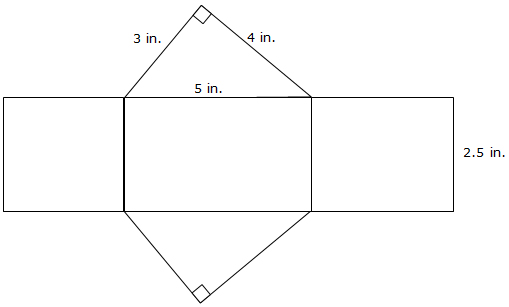
Triangular Prism:
Connecting Nets to Formulas
Now that you have explored nets of 3-dimensional figures, let's use those nets to generate formulas for surface areas of prisms, pyramids, and cylinders.
First, consider the net below for a rectangular prism. The bases of the prism are highlighted in blue. We know that the area of a rectangle is the product of the length and the width, so if we label the dimensions of each of the faces of the prism, we can calculate the surface area of the prism.
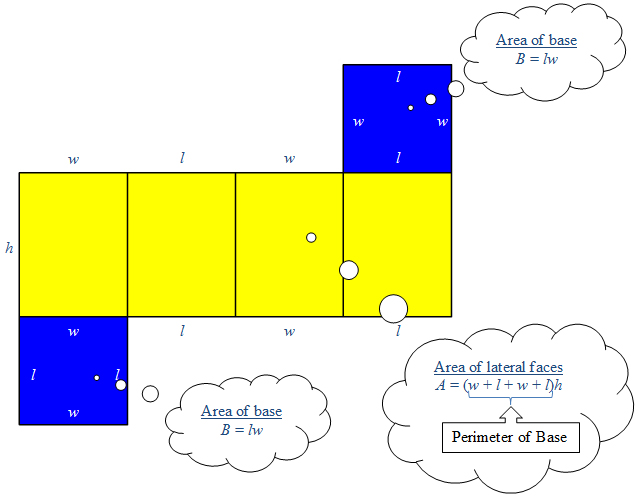
The diagram shows the lateral faces of the prism forming one big rectangle. The area of the big rectangle is found by adding the widths of all of the individual faces, the perimeter (P) of the prism, and then multiplying by the height.
In other words,
Lateral Area = Perimeter of Base × Height of Prism
Lateral Area = Ph
Next, find the area of one of the two congruent bases, area B. To find the total surface area, add the area of the large rectangle plus two times the area of the base, B.
In other words,
Total Surface Area = Lateral Area + 2 × Area of Base
Lateral Area = Ph + 2B
We can use similar logic for a pyramid.
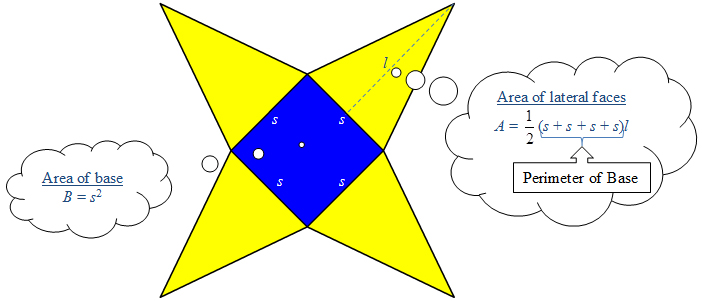
The area of the 4 lateral faces is found by adding the widths of all of the individual faces, the perimeter (P) of the base of the pyramid, and then multiplying by the height of the triangle, which is the slant height, l, of the pyramid.
In other words,
Lateral Area = × Perimeter of Base × Slant Height of Pyramid
Lateral Area = Pl
Next, find the area of the base, area B. To find the total surface area, add the area of the base, B, to the lateral area.
In other words,
Total Surface Area = Lateral Area + Area of Base
Lateral Area = Pl + B
For a cylinder, we can also develop formulas from the net.
The dimensions of the lateral surface are the circumference of the circle, 2πr, and the height of the cylinder, h.
In other words,
Lateral Area = Length of Rectangle × Width of Rectangle
Lateral Area = 2πrh
The bases of a cylinder are circles, so we can find the area of a circle using the formula A = πr2.
In other words,
Total Surface Area = Lateral Area + 2 × Area of Base
Total Surface Area = 2πrh + 2πr2

Summary
Being able to determine the surface area of a 3-dimensional figure is an important measurement skill. To determine the surface area, you can calculate the sum of the areas of particular faces or surfaces of a 3-dimensional solid, or use the lateral area and total surface area formulas.
Method 1: Sum of Areas of Faces/Surfaces
If you have a net, it is frequently easier to calculate the area of each figure (polygon or circle), and then add the areas together to get either the lateral area or total surface area.
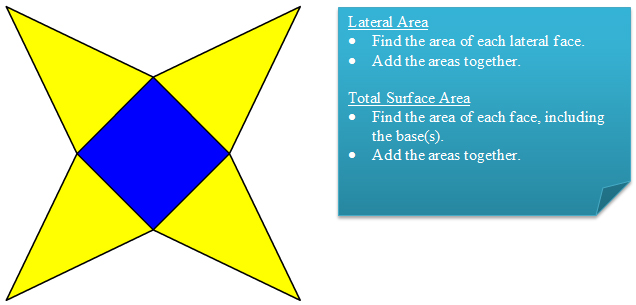
Method 2: Using the Formulas
If you have a figure with dimensions labeled, it may be easier to use the lateral area and surface area formulas.